Planted Clique Conjectures Are Equivalent
In this note, I will explain my favorite STOC’24 paper “Planed Clique Conjectures Are Equivalent”, a joint work with Shuichi Hirahara. I will explain the background, main results, and the description of our reductions. The detailed analysis and proofs are omitted here, but you can find them in the paper.
- link to STOC version
- link to full version
- link to slide
Background
In Planted Clique Problem, we are given a random graph obtained by the following procedure:
Sample a graph $G$ from the Erdős-Rényi model $G(n, 1/2)$ with $n$ vertices. Then, choose a set of $k$ vertices $C\subseteq [n]$ uniformly at random and add edges between all pairs of vertices in $C$, making $C$ a $k$-clique in $G$. The distribution of the resulting graph is denoted as $\PC(n, k)$.
The goal is to find the planted clique $C$ given a graph drawn from $\PC(n,k)$.
The complexity of finding the planted clique in a graph drawn from $\PC(n,k)$ crucially depends on the size $k$ of the planted clique.
- It is well known that the maximum clique in a random graph $G\sim G(n,1/2)$ is of size $(2+o(1))\log_2 n$ with high probability. Thus, if $k\le 2\log_2 n$, then we cannot find $C$.
- On the other hand, if $k\gg 2\log_2 n$, we can find $C$ with high probability by the brute-force search over all $k$-cliques in $G$.
Therefore, the threshold $k=2\log_2 n$ is the information-theoretic limit for solvability of the planted clique problem. However, the brute-force search for $k\gg2\log_2 n$ is not efficient. So the natural question is:
Can we find the planted clique $C$ given $G\sim\PC(n,k)$ when $k\gg 2\log_2 n$?
This question was initially studied by Jerrum[1] and Kučera[2]. Jerrum[1] proved that a class of algorithms based on Metropolis process cannot find the planted clique when $k\ll \sqrt{n}$. Kučera[2] showed that if $k\ge c\sqrt{n\log n}$ for a sufficiently large constant $c>0$, then vertices with top-$k$ largest degrees in $G$ form the planted clique $C$ with high probability. In a seminal work, Alon, Krivelevich, and Sudakov[3] presented a polynomial-time algorithm that finds the planted clique with high probability when $k\ge c\sqrt{n}$ for an arbitrary constant $c>0$.
Despite a long line of research from 1990s, no polynomial-time algorithm is known for Planted Clique Problem for $k\ll \sqrt{n}$. Moreover, several works have shown that Planted Clique Problem with $k\ll \sqrt{n}$ is hard against various natural classes of algorithms, including Lovász–Schrijver semidefinite programming hierarchy[4], sum-of-squares hierarchy[5], statistical query algorithms[6], and constant depth circuits[7].
This raises the conjecture asserting the hardness of Planted Clique Problem for $k\ll \sqrt{n}$.
Conjecture 1(Planted Clique Conjecture)
There exists a constant $\alpha>0$ such that for $k = n^{1/2-\alpha}$, no polynomial-time algorithm can find the planted clique $C$ from $G\sim\PC(n,k)$ with probability $2/3$, where the probability is taken over the choice of $G$.
Assuming Conjecture 1, we can see that Planted Clique Problem exhibits a computational-statistical gap: The information-theoretical threshold is $k=2\log_2 n$, whereas the computational threshold is $k=\sqrt{n}$. This kind of gap appears in a variety of problems in high-dimensional statistical inference.
Motivation of Planted Clique
Why do we care about the hardness of Planted Clique Problem? For computational complexity theorists, Planted Clique Problem can be seen as a natural average-case problem that is conjectured to be hard. Moreover, this problem can be seen as the average-case variant of the maximum clique problem, which is a well-known NP-hard problem.
In the area of high-dimensional statistics, Planted Clique Conjecture serves as a hypothetical hardness assumption for various statistical inference problems, including community detection[8], sparse PCA[9], and approximate Nash Equilibria[10], to name a few. Assuming Planted Clique Conjecture, we can prove computational lower bounds for these problems.
Interestingly, based on Planted Clique Conjecture, we can construct a one-way function, a fundamental building block of cryptography [11]. Roughly speaking, a one-way function is a function $f$ that can be easy to compute $f(x)$ given $x$ but hard to invert $x$ for given $f(x)$ for random $x$. For example, consider a function $f(G,C)$ that outputs the graph obtained by making $C$ a clique in $G$, which is easy to compute given $G$ and $C$. If $G$ is drawn from $G(n,1/2)$ and $C$ is a random $k$-vertex set, then distribution of $f(G,C)$ coincides with $\PC(n,k)$. Thus, assuming Planted Clique Conjecture, it is hard to invert $f(G,C)$ for random $G$ and $C$. A variant of Planted Clique Problem is shown to be useful in the context of secret sharing[12] and public-key cryptography[13].

Planted Clique Conjectures Are Equivalent
In my STOC’24 paper with Shuichi [14], we show that several variant of Planted Clique Conjectures are equivalent. The variants are as follows:
Decision version: In the decision version of Planted Clique Problem, our task is to distinguish two distributions: $\PC(n,k)$ and $G(n,1/2)$. Specifically, we are given a graph $G$ that is drawn from either $\PC(n,k)$ or $G(n,1/2)$, and we are asked to decide which distribution from which $G$ is drawn. We say that an algorithm $A$ has advantage $\beta$ if
\[\begin{align*} \left|\Pr_{G\sim\PC(n,k)}[A(G)=1] - \Pr_{G\sim G(n,1/2)}[A(G)=1]\right| \geq \beta. \end{align*}\]Our goal is to design an algorithm with as high advantage as possible.
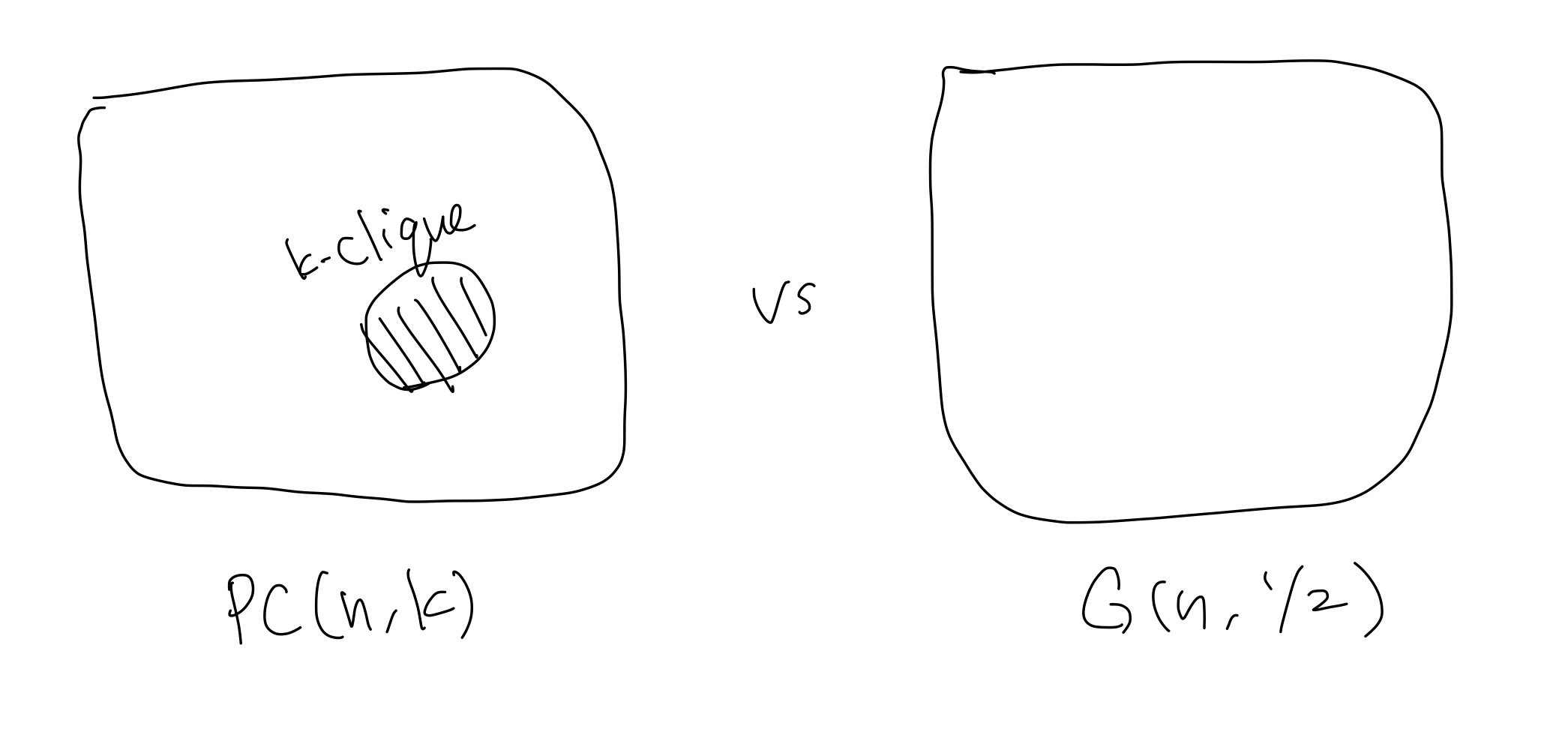
Search version: In the search version of Planted Clique Problem, we are given a graph $G$ that is drawn from $\PC(n,k)$, and our task is to find the planted clique $C$ (this coincides with the definition above). We say that an algorithm $A$ has success probability $\beta$ if
\[\begin{align*} \Pr_{G\sim\PC(n,k)}[A(G)=C] \geq \beta, \end{align*}\]where $C$ denotes the planted clique in $G$. Conjecture 1 says that any polynomial-time algorithm has success probability at most $2/3$ for $k=n^{1/2-\alpha}$.
In view of this, the formal statement of “Planted Clique Conjecture” relies on
- whether we care about the decision version or search version, and
- the choice of the parameter $\beta$ (the success probability or advantage).
In our paper [14], we show that the choice above (decision or search, and the choice of $\beta$) does not matter for a wide range of $\beta$. Roughly speaking, we show that
If one can distinguish $\PC(n,n^{1/2-\alpha})$ and $G(n,1/2)$ with advantage $\Omega(1)$ for some $\alpha>0$, then one can find the planted clique $C$ from $\PC(n,n^{1/2-\alpha’})$ with success probability $1-\exp(-n^{\Omega(1)})$ for some $\alpha’>0$.
Below is the precise statement of our result.
Theorem 2 (informal)
The following statements are equivalent:
- There exist a constant $\alpha>0$ and a polynomial-time algorithm $A$ that finds the planted clique $C$ from $G\sim\PC(n,n^{1/2-\alpha})$ with probability $2/3$.
- There exist constants $\alpha,\gamma>0$ and a polynomial-time algorithm $A$ that finds the planted clique $C$ from $G\sim\PC(n,n^{1/2-\alpha})$ with probability $1-\exp(-n^\gamma)$.
- There exist constants $\alpha,\gamma>0$ and a polynomial-time algorithm $A$ that finds the planted clique $C$ from $G\sim\PC(n,n^{1/2-\alpha})$ with success probability $1/n^\gamma$.
- There exist a constant $\alpha>0$ and a polynomial-time algorithm $A$ that distinguishes $\PC(n,n^{1/2-\alpha})$ from $G(n,1/2)$ with advantage $1/3$.
- There exist constants $\alpha,\gamma>0$ and a polynomial-time algorithm $A$ that distinguishes $\PC(n,n^{1/2-\alpha})$ from $G(n,1/2)$ with advantage $1-\exp(-n^\gamma)$.
- There exist constants $\alpha,\gamma>0$ and a polynomial-time algorithm $A$ that distinguishes $\widetilde{\PC}(n,n^{1/2-\alpha})$ from $G(n,1/2)$ with advantage $k^{2+\gamma}/n$.
Here, the distribution $\widetilde{\PC}(n,k)$ is called binomial-$k$ model, defined as the distribution of the following random graph: Sample $G\sim G(n,1/2)$ and let $C\subseteq [n]$ be a random subset that contains each vertex with probability $k/n$ independently. Then, add edges between all pairs of vertices in $C$, making $C$ a clique in $G$.
The first three statements says that the choice of the success probability $\beta$ does not matter for the search version of Planted Clique Conjecture for any $1/\poly(n) \le \beta \le 1-\exp(-\poly(n))$. Similarly, the last three statements say that the choice of the advantage $\beta$ does not matter for the decision version of Planted Clique Conjecture as long as $k^{2+\gamma}/n \le \beta \le 1-\exp(-\poly(n)) $.
In the binomial-$k$ model, the size of the planted clique is random with mean $k$. But the Chernoff bound yields that the clique size is concentrated around $k$ with high probability. So these two models (binomial-$k$ and fixed-$k$) are essentially equivalent (but I don’t know how to prove that).
As an immediate but interesting corollary, we can obtain the following statement:
Corollary 3 (informal)
If there is a polynomial-time algorithm that distinguishes $\widetilde{\PC}(n,k)$ and $G(n,1/2)$ with advantage $k^{2+\gamma}/n$ for some constant $\gamma>0$, then there is a polynomial-time algorithm that finds the planted clique for a graph drawn from $\PC(n,n^{1/2-\alpha’})$ with advantage $1-\exp(-n^{\gamma’})$ for some constants $\alpha’,\gamma’>0$.
Indeed, by counting the number of edges, we can distinguish $\widetilde{\PC}(n,k)$ with $G(n,1/2)$ with advantage $\Omega(k^/n)$ (see, e.g., Luca’s blog). Therefore, Corollary 3 implies that assuming Planted Clique Conjecture, the edge counting algorithm is almost optimal for the decision version of Planted Clique Problem.
Corollary 3 improves the search-to-decision reduction by Alon et al.[15]. Informally speaking, they showed how to reduce finding the planted clique in $\PC(n,k)$ to distinguishing $\PC(n,k)$ and $G(n,1/2)$ with advantage $1-o(n)$.
Later work: A very recent paper [16] further closed the gap between $k^{2+\gamma}/n$ and $k^2/n$ using a more sophisticated analysis. Actually, they showed that assuming Conjecture 1, a low-degree algorithm achieves an optimal advantage for the decision version of Planted Clique Problem.
Techniques
The key ingredient in our proof is two kinds of reductions: embedding reduction and shrinking reduction. These reductions are aimed to boost the advantage or success probability of an algorithm.
Embedding Reduction
This reduction is introduced in our previous work [17]. The idea is to randomly embed the planted clique $C$ into a larger Erdős–Rényi graph $G(N,1/2)$.
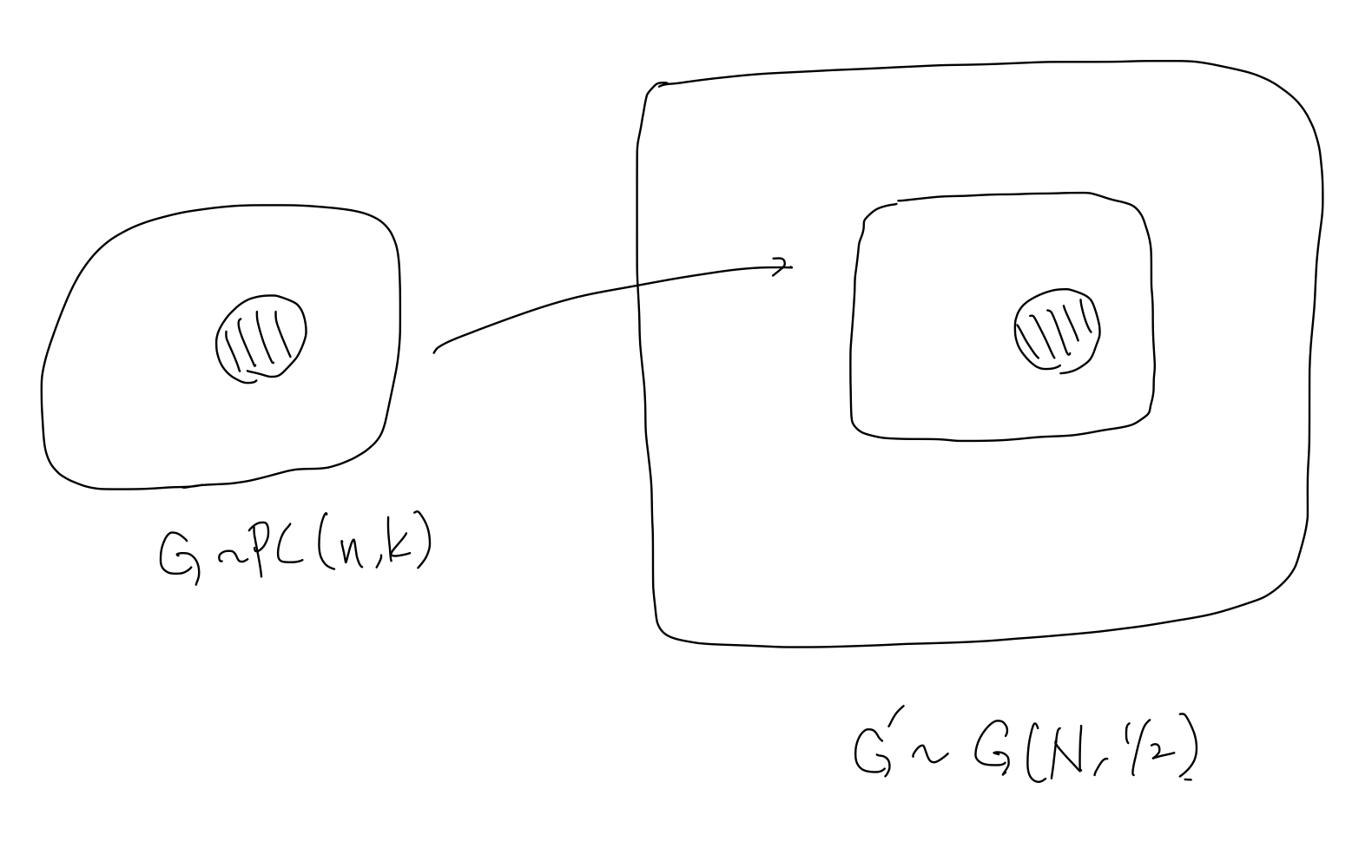
Note that the distribution of the resulting graph is identical to $\PC(N,k)$. If we set $N = n^{1+o(1)}$ and $k = n^{1/2-\alpha}$, then the size of the planted clique $C$ is $k = n^{1/2-\alpha} = N^{1/2-\alpha-o(1)}$.
Let $\calO$ be an algorithm that finds the planted clique in $G(N,k)$ with small success probability. Consider the following oracle algorithm $A^{\calO}$:
Algorithm $A_{\mathrm{emd}}^{\calO}(G,N)$.
Let $G\sim\PC(n,k)$ be the input and $N$ is a parameter.
- Obtain $G’$ by the embedding reduction above.
- If $\calO(G’)$ is a $k$-clique $C’$, then, we can find the original clique and output it.
- Repeat 1-2 for $\poly(n)$ times. If we cannot find a $k$-clique, then output “failure”.
Using this, we can boost the success probability of $\calO$ as follows:
Theorem 4 (Theorem 6.8 in the full version)
Suppose that $\calO$ finds the planted clique in $G(N,k)$ with success probability $\varepsilon$ and let $\delta>0$ be any parameter. If $N$ satisfies $N\ge n\cdot \log(1/\varepsilon)/\delta^2$, then the oracle algorithm $A^{\calO}_{\mathrm{emb}}(G,N)$ finds the planted clique in $G(n,k)$ with success probability $1-\delta$.
If we set $\varepsilon = 1/\poly(n)$ and $\delta=1/3$, we can say that the oracle algorithm $A^{\calO}_{\mathrm{emb}}(G,N)$ finds the planted clique in $G(n,k)$ with success probability $2/3$ given an oracle $\calO$ that finds the planted clique in $G(N,k)$ with success probability $1/\poly(n)$. This implies Item 3 $\Rightarrow$ Item 1 in Theorem 2.
A similar boosting result also holds for the decision version, where we boost the advantage by taking the majority of the answers.
Algorithm $D_{\mathrm{emd}}^{\calO}(G,N)$.
Let $G$ be the input $n$-vertex vector and $N$ is a parameter.
- Obtain $G’$ by the embedding reduction above.
- Let $b\leftarrow \calO(G’)$.
- Repeat 1-2 for $\poly(n)$ times and output the majority of the answers $b$.
Theorem 5 (Theorem 6.9 in the full version)
Suppose that $\calO$ distinguishes $\PC(N,k)$ and $G(N,k)$ with advantage $\varepsilon$ and let $\delta>0$ be any parameter. If $N$ satisfies $N\ge n\cdot \log(1/\varepsilon)/(\delta^2\varepsilon^2)$, then the oracle algorithm $A^{\calO}_{\mathrm{emb}}(G,N)$ finds the planted clique in $G(n,k)$ with success probability $1-\delta$.
Unfortunately, we cannot set $\varepsilon=1/\poly(n)$ here (for example, if we set $\varepsilon=1/n$, then we would have $N=n^3$, which is too big).
Shrinking Reduction
The main drawback of the embedding reduction is that we cannot set $\delta$ to be small. This is because the size of the large graph is $N\ge 1/\delta^2$. In order to deal with small $\delta$, we shall use a different reduction called shrinking reduction.
The reduction is very simple: Given an $M$-vertex graph, choose $m<M$ distinct vertices randomly and take the subgraph induced by these vertices.
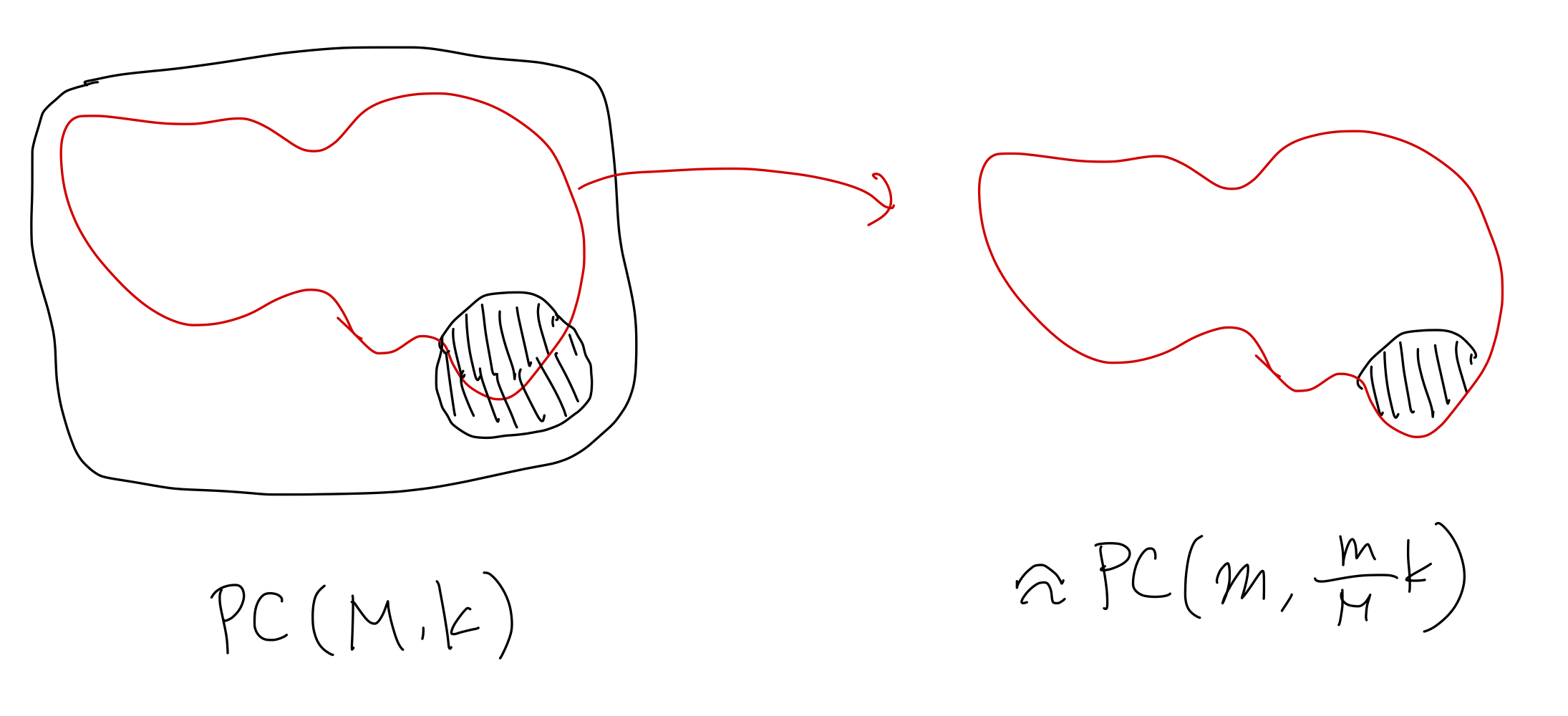
Let $G$ be the original graph and $G’$ be the resulting graph. If $G$ is drawn from $G(M,1/2)$, then the distribution of $G’$ is $G(m,1/2)$.
On the other hand, if $G$ is drawn from $\PC(M,k)$ with planted clique $C\subseteq[M]$, then the distribution of $G’$ is $\PC(m,k’)$, where $k’$ is the number of vertices in the planted clique included in the vertices of $G’$. More precisely, let $S\subseteq[M]$ be set of the chosen $m$ vertices in this reduction and $C\subseteq[M]$ be the planted clique. Then, the resulting graph has clique of size $k’=\abs{S\cap C}$. Note that $k’$ is a random variable. The distribution of $k’$ is identical to the hypergeometric distribution with mean $\frac{m}{M}k$. Actually, this distribution is statistically close to the binomial distribution $\mathrm{Bin}(m,k/M)$. Conditioned on $k’$ the distribution of $G’$ is precisely $\PC(m,k’)$. Therefore, the resulting graph has a clique of size (statistically close to) $\mathrm{Bin}(m,k/M)$, meaning that the graph is statistically close to $\widetilde{\PC}(n,k)$.
Likewise as the embedding reduction, we can boost the success probability or advantage of an algorithm using this reduction. In the following, we focus on the decision version.
Algorithm $D_{\mathrm{shr}}^{\calO}(G,m)$.
Let $G$ be the graph over $M$ vertices and $m$ is a parameter.
- Choose $m$ vertices uniformly at random from $G$ and let $G’$ be the subgraph induced by $m$.
- Output $\pi(G’)$, where $\pi\colon[m]\to[m]$ is a random permutation.
- Let $b\leftarrow\calO(G’)$.
- Repeat 1-3 for $\poly(m)$ times and output the majority of the answers $b$.
Theorem 6 (Theorem 6.9 in the full version)
Let $\calO$ be an algorithm that distinguishes $\widetilde{\PC}(m,k’)$ and $G(m,1/2)$ with advantage $\varepsilon$, where $k’=(m/M)\cdot k$. For any $\delta>0$, let $m$ be a parameter such that $m\le M\cdot \varepsilon / \sqrt{\log(1/\delta)}$. Then, the algorithm $A^{\calO}_{\mathrm{shr}}(G,m)$ distinguishes $\PC(M,k)$ and $G(M,1/2)$ with advantage $1-\delta$.
The key point is that the parameter $m$ depends logarithmically on $1/\delta$, which enables us to set $\delta = \exp(-M^{o(1)})$. On the other hand, $m$ depends polynomially on $1/\varepsilon$. So we need $\varepsilon = M^{-o(1)}$. Fortunately, we can deal with this case thanks to the embedding reduction!
Although $\PC(n,k)$ and $\widetilde{\PC}(n,k)$ are very similar, we are not aware of any computational equivalence between them. But we can prove reduce search problem over $\widetilde{\PC}(m,1.1k)$ to the search problem over $\PC(m,k)$ with a cost of success probability.
Lemma 7 (Modification of Lemma 5.7 in the full version)
Let $k=\omega(\log m)$. If there is a polynomial-time algorithm that finds the planted clique in $\PC(m,k)$ with success probability $1-\delta$, then there is a polynomial-time algorithm that finds the planted clique in $\widetilde{\PC}(m,1.1k)$ with success probability $1-m\delta-m^{-\omega(1)}$.
Proof sketch. Let $\calO$ be the algorithm that finds the planted clique in $\PC(m,k)$ with success probability $1-\delta$. Let $G\sim\widetilde{\PC}(m,1.1k)$ be the input. Since the distribution of the planted clique size is $\mathrm{Bin}(m,1.1k/m)$, the Hoeffding bound implies that the clique size is at least $k$ with probability $1-m^{-\omega(1)}$.
The idea of the reduction is simple: Let $v_1,\dots,v_m$ be the vertices of $G$. For each $i\in[m]$, let $G_i$ be the graph obtained by resampling edges touching ${v_1,\dots,v_i}$. Run the oracle $\calO$ on each $G_i$. If the oracle finds a $k$-clique in $G_i$, then it is a subclique of the planted clique $C$ in $G$ (with high probability). So we can recover the whole clique in $G$.
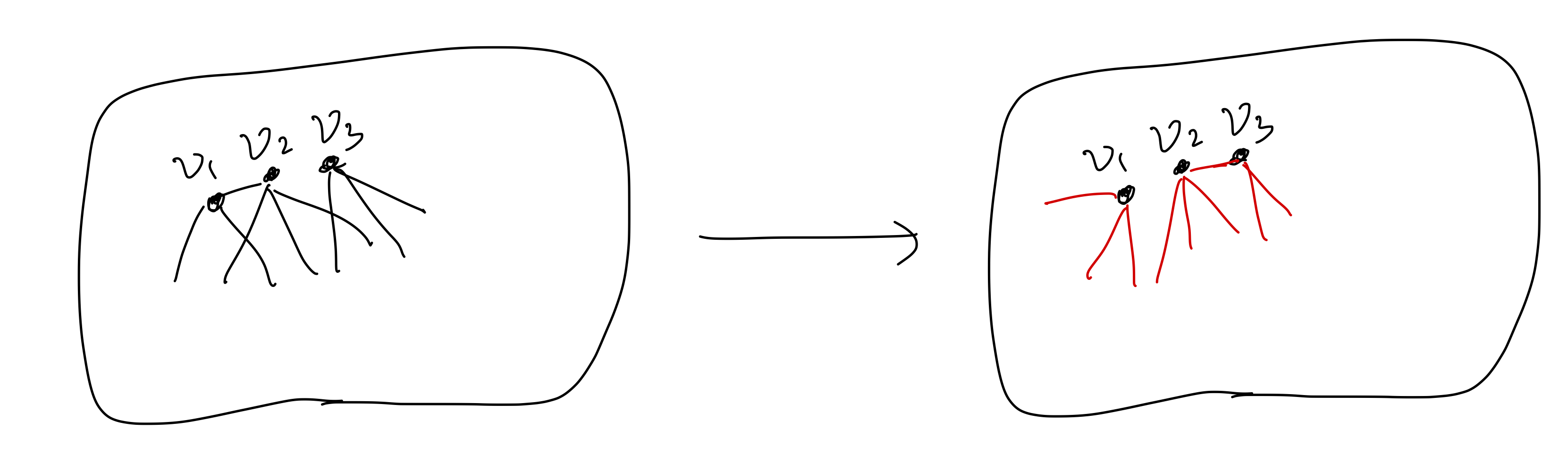
In $G_i$, the size of the planted clique is $k - \abs{\qty{v_1,\dots,v_i}\cap C}$. Therefore, the clique size decreases by at most 1 for each $i$. For some $j$, the marginal distribution of $G_{j}$ is $\PC(m,k)$ and the algorithm $\calO$ finds the planted clique in $G_{j}$ with success probability $1-\delta$. By the union bound over $i$, the total success probability is at least $1-m\delta$. $\square$
Unfortunately, we are not aware of how to prove a analogous lemma for the decision version.
References
- Mark Jerrum. 1992. Large Cliques Elude the Metropolis Process. Random Structures & Algorithms, 3(4), 347–360. doi: 10.1002/rsa.3240030402.
- Luděk Kučera. 1995. Expected Complexity of Graph Partitioning Problems. Discrete Applied Mathematics, 57, 2-3, 193–212. doi: 10.1016/0166-218X(94)00103-K.
- Noga Alon, Michael Krivelevich, and Benny Sudakov. 1998. Finding a Large Hidden Clique in a Random Graph. Random Structures & Algorithms, 13(3-4), 457–466. doi: 10.1002/(SICI)1098-2418(199810/12)13:3/4<457::AID-RSA14>3.0.CO;2-W.
- Uriel Feige and Robert Krauthgamer. 2003. The Probable Value of the Lovász–Schrijver Relaxations for Maximum Independent Set. SIAM Journal of Computing, 32(2), 345–370. doi: 10.1137/S009753970240118X.
- Boaz Barak, Samuel B. Hopkins, Jonathan A. Kelner, Pravesh K. Kothari, Ankur Moitra, and Aaron Potechin. 2019. A Nearly Tight Sum-of-Squares Lower Bound for the Planted Clique roblem. SIAM Journal on Computing, 48(2), 687–735. doi:10.1137/17M1138236.
- Vitaly Feldman, Elena Grigorescu, Lev Reyzin, Santosh S. Vempala, and Ying Xiao. 2017. Statistical Algorithms and a Lower Bound for Detecting Planted Cliques. Journal of the ACM, 64(2), 8:1–8:37. doi: 10.1145/3046674.
- Benjamin Rossman. 2008. On the constant-depth complexity of k-clique. In Proceedings of the Symposium on Theory of Computing (STOC), 721–730. doi:10.1145/1374376.1374480.
- Bruce Hajek, Yihong Wu, and Jiaming Xu. 2015. Computational Lower Bounds for Community Detection on Random Graphs, In Proceedings of Conference on Learning Theory (COLT), PMLR 40:899-928.
- Quentin Berthet, Philippe Rigollet. 2013. Complexity Theoretic Lower Bounds for Sparse Principal Component Detection. In Proceedings of Conference on Learning Theory, PMLR 30:1046-1066.
- Lorenz Minder and Dan Vilenchik. 2009. Small Clique Detection and Approximate Nash Equilibria. In Proceedings of Approximation, Randomization, and Combinatorial Optimization (APPROX-RANDOM). doi:10.1007/978-3-642-03685-9_50.
- Ari Juels and Marcus Peinado. 1997. Hiding cliques for cryptographic security. Designs Codes and Cryptography, 20(11), doi:10.1023/A:1008374125234.
- Damiano Abram, Amos Beimel, Yuval Ishai, Eyal Kushilevitz, and Varun Narayanan. 2023. Cryptography from Planted Graphs: Security with Logarithmic-Size Messages. In Proceedings of Theory of Cryptography (TCC), doi:10.1007/978-3-031-48615-9_11.
- Benny Applebaum, Boaz Barak, and Avi Wigderson. 2010. Public-Key Cryptography from Different Assumptions. In Proceedings of Symposium on Theory of Computing. doi:10.1145/1806689.1806715.
- Shuichi Hirahara and Nobutaka Shimizu. 2024. Planted Clique Conjectures Are Equivalent. In Proceedings of Symposium on Theory of Computing (STOC). doi:10.1145/3618260.3649751.
- Noga Alon, Alexandr Andoni, Tali Kaufman, Kevin Matulef, Ronitt Rubinfeld, and Ning Xie. 2007. Testing k-wise and almost k-wise independence, In Proceedings of Symposium on Theory of Computing (STOC), doi: 10.1145/1250790.1250863.
- Ansh Nagda and Prasad Raghavendra. 2025. On optimal distinguishers for Planted Clique. arXiv:2505.01990.
- Shuichi Hirahara and Nobutaka Shimizu. 2023. Hardness Self-Amplification: Simplified, Optimized, and Unified. In Proceedings of Symposium on Theory of Computing (STOC). doi:10.1145/3564246.3585189.