コラム: NP困難の定義と歴史

• コラム: NP困難の定義と歴史
  • 概要
  • 帰着の種類
  • およそ全ての文脈で共通する定義
  • 判定問題のNP困難性
  • 探索問題のNP困難性
  • 結論
  • 余談: 用語の標準化の歴史

概要

一般に「NP困難」とは, 「NPに属する任意の問題に対してそれ以上に難しい」という性質を指すが, 用いる帰着の種類によってその定義が変わってくる. このページでは, 様々な分野の標準的な教科書ではどの定義を採用しているかについて調査してまとめる. また, 「NP困難(NP-hard)」という用語の歴史について説明する. この内容はGarey & Johnson本 (1979) のSection 5.2に基づく. このSection 5.2の内容は計算量理論の歴史について非常に面白い内容なので, 興味がある人は是非原著を読んで欲しい.

本稿では具体的には

• 判定問題を対象とする理論 (主に計算量理論)
• 探索問題を対象とする理論 (組合せ最適化理論など)

の二つの文脈におけるNP困難性の定義を, これらの分野における以下の標準的な教科書でどう扱っているかを調査した:

• Computational Complexity: A Modern Approach, Arora and Barak, 2007 (計算量理論).
• Computational Complexity: A Conceptual Perspective, Goldreich, 2008 (計算量理論).
• Introduction to the Theory of Computation (3rd ed.), Sipser, 2012 (計算量理論).
• Computational Complexity, Papadimitriou, 2003 (計算量理論).
• Computers and Intractability: A Guide to the Theory of NP-Completeness, Garey and Johnson, 1979 (計算量理論).
• Mathematics and Computation: A Theory Revolutionizing Technology and Science, Wigdreson, 2019 (計算量理論)
• Combinatorial Optimization: Theory and Algorithms (6th ed.), Korte and Vygen, 2018 (組合せ最適化).

計算量理論以外の分野の調査は不十分なので, 今後も新たに調査したらその都度文献を増やしていく.

---

帰着の種類

Cook帰着とKarp帰着の定義をまとめる. 本来であればオラクルアルゴリズムの定義を示すべきだが, 本筋から外れるのでここでは省略する.

定義1

判定問題$L_1,L_2$を考える. ここでは判定問題は指示関数と同一視する.

• $L_1$ が $L_2$ に Cook帰着できる とは, $L_1$ を解く多項式時間オラクルアルゴリズム $A^{L_2}$ が存在することをいう.
• $L_1$ が $L_2$ に Karp帰着できる とは, ある多項式時間アルゴリズム $f\colon \binset^{\ast} \to \binset^{\ast}$ が存在して, 任意の $x \in \binset^{\ast}$ に対して $x \in L_1 \Leftrightarrow f(x) \in L_2$ が成り立つことをいう.

なお, Cook帰着の定義においてオラクルアルゴリズムの計算量を多項式時間に限らないものを考えるときは Turing帰着 と呼ぶこともある. すなわち Cook帰着は多項式時間Turing帰着と同義である.

Karp帰着では$L_1$を解くオラクルに1回しかアクセスできないのに対してCook帰着では多項式回アクセスできるため, Cook帰着の方が一般的で強力な帰着である. 一方で帰着を用いて定義された計算量クラスの性質を調べるときは, 単純な構造を持つ帰着の方が扱いやすいため, Karp帰着のような制限的な帰着が好まれることが多い. 後述するが, 探索問題に対してKarp帰着のような制限的な帰着としてLevin帰着を考えることができ, 探索問題の計算量の文脈(PPADなど)ではこの帰着が好まれている.

---

およそ全ての文脈で共通する定義

クラスNP や NP完全 は決定問題にのみ以下のように定義される.

定義2

NPに属する任意の判定問題 $L’$ が 判定問題 $L$ にKarp帰着でき, さらに $L\in\mathsf{NP}$ であるとき, $L$ は NP完全という.

Cook (1971) はNPに属する全ての問題が Cook帰着 の意味でSATに帰着できることを示した. 翌年にKarp(1972)が現在の形でNP完全性を初めて明確に定義した. 彼はさらにCookの結果がKarp帰着の下でも成り立つことを示し, 様々な問題のNP完全性を示した. この論文で示された21個のNP完全問題は現在でもKarpの21 NP完全問題として知られている.

より一般の(判定問題とは限らない)問題のクラス $\calC$ を考えたとき, $\calC$ に属する任意の問題がある問題 $\Pi$ に帰着でき, さらに$\Pi$自身が$\calC$に属するとき, $\Pi$を$\calC$完全と呼ぶ. ここで考える帰着はKarp帰着のような「1回しかオラクルにアクセスできない」帰着であることがほとんどであり, Cook帰着のような「複数回オラクルにアクセスできる」帰着はあまり使われない.

---

判定問題のNP困難性

一般には判定問題 $L$ は, $\mathsf{NP}$ に属する任意の問題に対してそれ以上に難しいとき, NP困難であるといわれる. ここでの「それ以上に難しい」という性質を帰着の概念を用いて定義される. ここでKarp帰着を使うかCook帰着を使うかによって二つのNP困難性が定義できる. 前者をKarp型, 後者をCook型と呼ぶことにする (これらの用語は本稿のローカルな呼称である).

定義3

• NPに属する任意の判定問題 $L’$ が判定問題 $L$ にKarp帰着できるとき, $L$ は Karp型NP困難であるという.
• NPに属する任意の判定問題 $L’$ が判定問題 $L$ にCook帰着できるとき, $L$ はCook型NP困難であるという.

判定問題に対してNP完全性とは別にNP困難性を考える動機は, NPよりも上位の階層の判定問題のクラス (PSPACEやPHなど) に対して「NPと同じかそれ以上に難しい」という性質を捉えたいからである.

この定義に基づくと, 計算量理論では以下のとても重要な差異が発生する:

coNP完全な問題はCook型NP困難であるが, $\mathsf{NP}\ne\mathsf{coNP}$ (成り立つと広く信じられている予想) の下ではKarp型NP困難ではない.

すなわち, 「回路$C\colon\binset^n\to\binset$ に対して充足可能割り当てが存在しないならYes, そうでないならNo」というcoNP完全な判定問題がNP困難かどうかが変わってしまう.

面白いことにKnuthは The Art of Computer Programming (vol. 4) の初版では判定問題のNP困難性をKarp型で定義していたが, 後にCook型で定義するべきであると主張している. これはcoNP完全な判定問題は任意のNPに属する問題以上に難しいためNP困難であるとするのが自然であると彼は捉えたからである (情報源: Garey & Johnson, Section 5.2).

---

探索問題のNP困難性

探索問題とは, 関係 $R\subseteq\binset^{\ast}\times\binset^{\ast}$ によって定まる問題であり, 直感的には「入力 $x\in\binset^{\ast}$ が与えられたとき, $(x,y)\in R$ を満たす $y\in\binset^{\ast}$ を何でも良いから一つ出力せよ」という問題である. 一般にこれを探索問題 $R$ と呼ぶ.

関数(アルゴリズム) $A\colon\binset^{\ast}\to\binset^{\ast}$ が $R$ を解くとは, 任意の $x\in\binset^{\ast}$ に対して

• $A$は$(x,y)\in R$を満たす $x$ が存在しないことを検出する (解なし), もしくは
• 出力 $A(x)\in\binset^*$ が $(x,A(x))\in R$ を満たす

ことをいう (つまりTuring機械とすると出力テープに書き込まれた文字列を$A(x)$と, 状態が拒否状態ならば「解なし」と判定したとみなす).

以下に探索問題の主要なサブクラスを示す.

• 任意の$x\in\binset^{\ast}$ に対して $(x,y)\in R$ を満たす $y$ が常に存在するとき, $R$を 全域探索問題 (total search problem) と呼ぶ.
• 探索問題に対してもNPのような概念を定義できる. 端的に言えば, NPの証拠を見つけよという探索問題である. フォーマルには与えられた$(x,y)$が$(x,y)\in R$かどうかを多項式時間で判定できる探索問題のクラスを FNP と呼ぶ.
• FNPに属する全域探索問題のクラスを TFNP と呼ぶ.

探索問題は最適化問題や数え上げ問題など, 判定問題を超えて様々な問題を表現できる. 特に, 判定問題も探索問題の特殊ケースとして表現できる. 具体的には, 判定問題 $L\colon\binset^{\ast}\to\binset$ に対して

\[R_L:=\set{(x,L(x))\colon x\in\binset^{\ast}}\]

とすれば判定問題として表現できる. この $R_L$ を便宜上, $L$の探索問題版 と呼ぶことにする (これらの用語は本稿のローカルな呼称である).

Karp帰着は判定問題にのみ定義できる帰着の概念であるため, 探索問題に対してKarp型NP困難という性質は定義できないが, Karp帰着の「1回しかオラクルにアクセスできない」という特徴を探索問題に自然に拡張することはでき, これをLevin帰着という. これはCook-Levinの定理のLevin(1973)が考えた帰着だからである.

定義4 (探索問題のLevin帰着とCook帰着)

二つの探索問題 $R_1,R_2\subseteq\binset^{\ast}\times\binset^{\ast}$ を考える.

• $R_1$が$R_2$にLevin帰着できるとは, 二つのある多項式時間アルゴリズム $f, g \colon \binset^{\ast}\to\binset^{\ast}$ が存在して, 任意の $x\in\binset^{\ast}$ と $(f(x),y’)\in R_2$ を満たす任意の $y’\in\binset^{\ast}$ に対して $(x,g(x,y’))\in R_2$ が成り立つことをいう.

• $R_1$が$R_2$にCook帰着できるとは, ある多項式時間オラクルアルゴリズム $A^{\mathcal{O}}$ が存在して, $R_2$ を解く任意のオラクル$\mathcal{O}\colon\binset^{\ast}\to\binset^{\ast}$ に対して $A^{\mathcal{O}}$ は $R_1$ を解く.

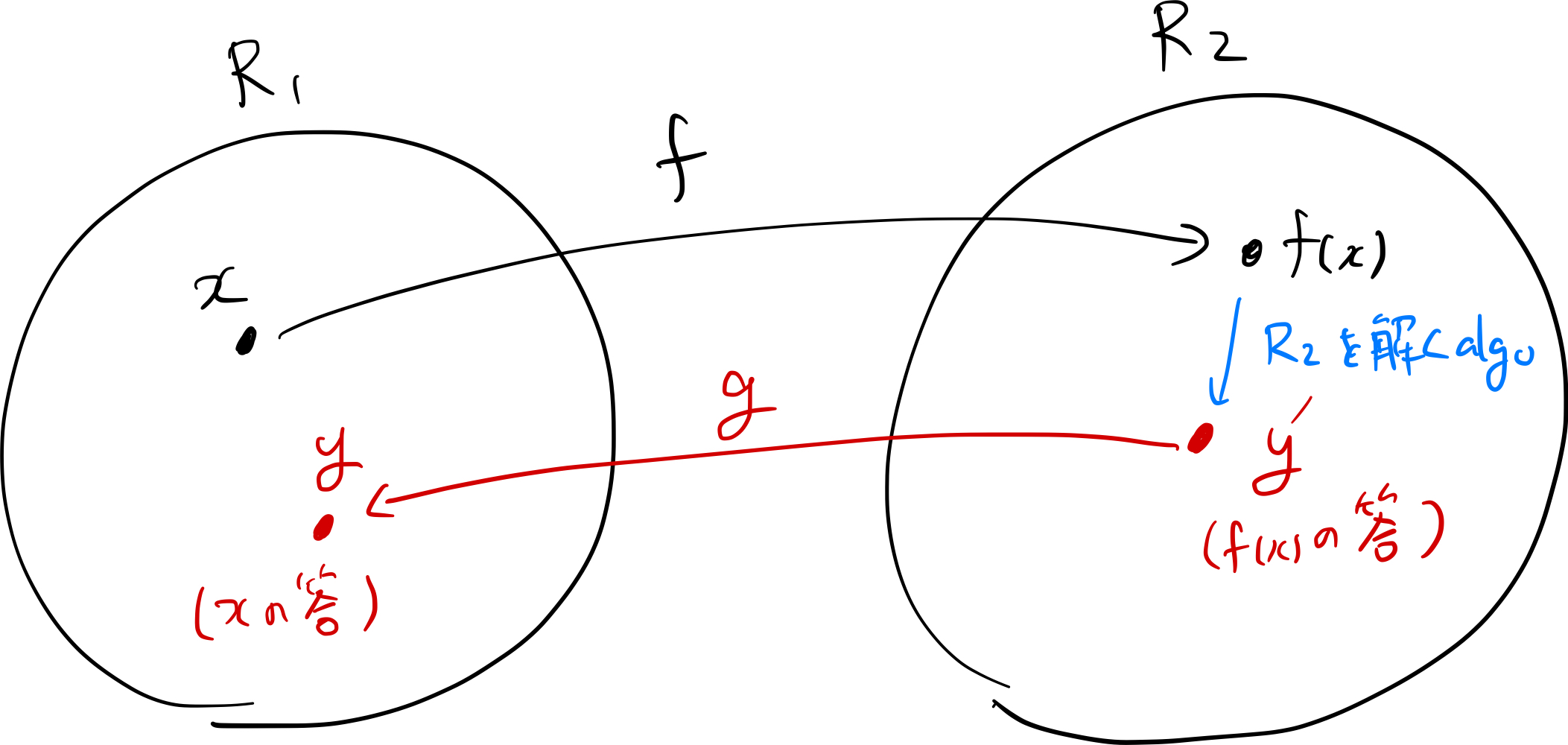
これらの帰着を用いれば, 判定問題と同様に探索問題 $R$ に対する二つのNP困難性を以下のように定義できる.

定義5 (探索問題のNP困難)

• 探索問題 $R$ は, FNPに属する任意の探索問題 $R’\in\mathsf{FNP}$ が $R$ にLevin帰着できるとき, Levin型NP困難であるという.

• 探索問題 $R$ は以下を満たすときCook型NP困難であるという: あるNP完全な判定問題 $L$ が存在して, $L$の探索問題版 $R_L$ が $R$ にCook帰着できる.

特に, FNPに属するLevin型NP困難な探索問題をFNP完全であるという. これはTFNPの有名なサブクラスであるPPAD完全性の定義にも引き継がれている.

---

結論

ここまでの話をまとめると, 判定問題や探索問題のNP困難性は自由度の高い帰着(Cook型)と1回しかオラクルアクセスできない制限的な帰着(Karp型やLevin型)の二つの定義が存在することになる. NP完全性やFNP完全性は常に制限的な帰着を用いて定義されるが, NP困難性に関しては両方の定義が存在する.

さて, NP困難の定義としてどちらを採用すべきかは文脈によって様々であるが, 以下の理由から, なんとなくCook型に統一した方が良さそうに思える.

• 例えば最適化問題の文脈では, 「最適値と与えられた閾値を比較せよ」という判定問題に二分探索を用いて帰着し, そのNP完全性を持って元の最適化問題はNP困難であるという議論がよく行われる. この場合, 最適化問題のNP困難性をLevin型で定義してしまうオラクルアクセスの回数が1回しか許されないのでこの議論が破綻してしまう.
• 前述したように, Knuthは The Art of Computer Programming (vol. 4) において, 判定問題のNP困難性をKarp型で定義していた. しかし後になってKnuthはKarp型ではなくCook型で定義するべきであると主張している. これはcoNPの箇所で述べたように, coNP完全な判定問題は任意のNPに属する問題以上に難しいためNP困難であるとするのが自然であると彼は捉えたからである.

ところが驚くべきことに様々な文献を調査した結果, 以下の事実が判明した:

• 現代の計算量理論の標準的な教科書のほとんどは判定問題のNP困難性をKarp帰着で定義し, 探索問題に対するNP困難性は定義していない (軽く触れる本はあった). Goldreichの本は $\mathsf{FNP}$ 完全性をLevin帰着の下で定義しているが, NP困難性には言及していない (書籍では $\mathsf{FNP}$ を $\mathcal{PC}$ と呼称している).
• 組合せ最適化の本と古典的な書籍 (Garey & Johnson, 1979) は探索問題に対するNP困難性をCook帰着で定義していた.

本タイトル	判定問題のNP困難性定義	探索問題のNP困難性定義	備考
Garey & Johnson (1979)	Karp型	Cook型	Section 5.1
Goldreich	Karp型	-	Section 2.3.1
Sipser	Karp型	-	演習問題7.34
Arora & Barak	Karp型	-	Definition 2.7
Papadimitriou	?	-	8.4.5にNP困難の言及があるが, 定義が曖昧
Wigderson (2019)	Karp型	-	-
Korte & Vygen	Cook型	Cook型	判定・探索を区別せずCook型で統一. 定義がかなり独特で, 雰囲気としてはPromise Total Search Problemに近い(Definition 15.3, 15.17).

もしかしたら私が探索問題のNP困難性の定義を書籍から見落としている可能性があるので, もし見つけた方がいらしたら教えていただけますと幸いです.

計算量理論はその研究対象は主に判定問題であり, 答えのYes/Noは非常に重要な意味を持つ. 従って, 変換前後で答えのYes/Noを保つKarp帰着は非常に親和性が高く, かつ帰着の構造が単純で扱いやすいのが理由であると考えられる (実際, Goldreichは自身の著作のDefinition 2.17の直後にそう述べている).

なお, 計算量理論では判定問題以外の問題 (例えば算術回路 $\mathsf{VNP}$ など) を扱うこともあり, その中ではその文脈独自の帰着を定義することによって $\mathsf{VNP}$困難といった概念を定義する. 要するに

計算量下界の専門的な文脈では場面ごとに帰着を定義してそれに基づいて困難性を明確に定めており, 判定問題ならKarp型NP困難性を考える. 一方で計算量下界よりも上界(効率的なアルゴリズム設計)をメインとする文脈では判定問題に拘らず, 従ってKarp帰着を考える特段の理由がないのでほぼ, 全ての状況下でNP困難性をCook型で定義している.

ということになる. おそらく幅広い分野で最も主流な定義はCook型NP困難性であるため, 計算量理論の専門的な論文執筆もしくは講義をしない限りはCook型NP困難性をNP困難と呼ぶのが無難であろう.

---

余談: 用語の標準化の歴史

この説の内容はGarey & Johnson (1979) のSection 5.2に基づく. この節で計算量理論のNP-completeとNP-hardの命名について非常に面白い逸話が書いてあったので紹介する.

数学の数多の概念がそうであったように, NP-completeとNP-hardの概念もまた, 様々な論文でそれぞれ別々の呼称が存在した. 最も最初に明確に定義されたのがKarp(1972)であり, その中では明確にNP-completeという用語が記されている. 一方でSahni(1974)では, 今でいうNP完全を P-hard (Definition 4), Cook型NP困難な探索問題を P-Complete (Definition 6)呼んでいた.

現在主流の用語が広まったのはKnuthによるところが大きい. 彼がThe Art of Computer Programming (vol. 4) を執筆する際に計算量の当時の専門家を集めて「どの命名が良いか」について投票を行い議論したようである. まず彼はP-hardの候補を棄却し, 三つの命名に対しどれが良いか投票したようであるが, どうやらその全ては一旦棄却され, 専門家の間で議論が始まったようである.

中には冗談混じりにPET problemが良いだろうという意見が出たらしい. PETは “probably exponential time” の略である. 一方で仮に $\mathsf{P}=\mathsf{NP}$ であった場合は “previously exponential time” の略とすれば良いからである.

上記の命名は全て判定問題のNP困難性についての議論であり, 著者が知る限り, 初めて探索問題に対して今の形のCook型のNP困難性を明確に定義したのは実はGarey & Johnson (1979) と思われる.

ただ, NPの性質を持つ探索問題に対してある種のNP困難性はもっと前のLevin(1973)で行われていた. 探索問題 $R\subseteq\binset^{\ast}\times\binset^{\ast}$ がNPの性質を持つとは, 与えられた $(x,y)$ に対して $(x,y)\in R$ かどうかの判定が多項式時間でできることを意味する (現代の計算量理論ではこの探索問題のクラスは $\mathsf{FNP}$と呼ばれる).

よく知られた事実であるが, 実はCook(1971)とは独立にLevin(1973)もまた独自にクラス$\mathsf{FNP}$ を sequential search type と呼び, これに対して「NP困難 (universal sequential search problem)」な問題を特定している. 当時は冷戦下であったため彼らの間に交流はなかったのだが, 実はソ連でも 本質的に全探索を必要とする問題 (perebor) についての研究が行われていたようである (Arora & Barak). 原著論文はロシア語であるが2024年にFortnowによる英訳を見ると, Definition 1でまさにNP証拠の探索問題に該当する問題をsequential search problemと呼び, Definition 2で非常に制限的な帰着を考えていることがわかる. この帰着では帰着先の問題を解くオラクルを呼び出せる回数は一回に制限されているため, Cook帰着よりはKarp帰着に近いものと思われる.

従って, 探索問題そのもののNP困難性はLevin(1973)で(非常に制限された帰着の下で)取り組まれていたが, より一般のTuring帰着に基づく現代でもよく使われるNP困難性の定義はGarey & Johnson (1979) で与えられたと思われる.